
シマウマさんを狙うワニさん!最短で辿りつくには何秒かかりますか?
イギリスのスコットランドで行われた統一試験SQAに出題された数学の問題が「難問すぎる」として国内で大顰蹙を買っています。16歳の学生たちに絶望感を味わわせた出題内容を見てみましょう。
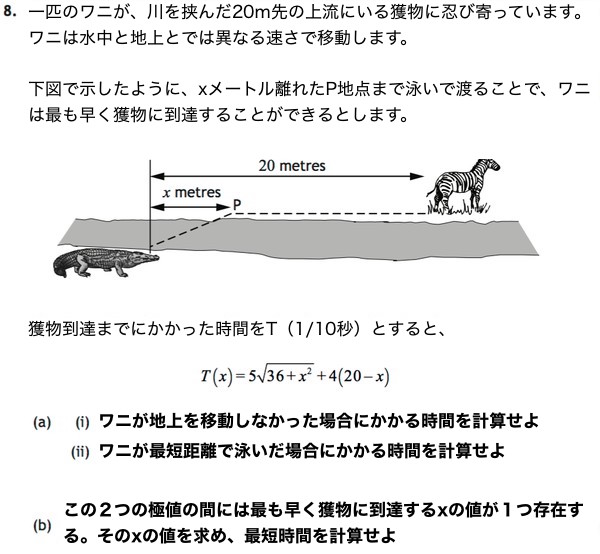
こちらがその難問
<海外の反応>
式に目をやった瞬間に頭脳が停止したわwww数学は苦手なんだよなぁ〜。
こんな意味のわからない書き方するとか、出題者はもうこれ以上テストに関んな。
これ受けたけど、ワニの問題は本当に不愉快だったわ。求めてるのは時間なのに・・なんで私の答えマイナスになったのよ!!
↑俺なんか、ワニさんウサイン・ボルトよりも早く走ってたぞwwwwww
シマウマは当然走って逃げるだろうから、ワニが走る距離も増えるんだが!
こういう意味のない問題出すぐらいだし、教育システムが破綻してるのは明らかね。卵の茹で方とかエンジンのオイルチェックとか、もっと有用なことを勉強させたらいいのに。
本年度の数学試験は全体的に難問揃いだったのですが、特にこの”ワニの問題”がその難しさを象徴していたと話題に。このような問題が扱われたことに関して「不公平だ」「これを解くのは不可能だ」とする声は大きく、実に1万4,000人を超える人がSQAを糾弾する署名運動に参加しています。
学校職員のローガン・フレイザー氏は学生に同情。このように語っていました。
「この不可能とされる問題にぶち当たり、ショックや狼狽を覚えた学生が多かった。過去14年間分の過去問を分析してきたが、この難易度に達した試験は見たことがない。涙ながらに試験会場を去った学生達の多さは例年以上だった」
解答
a-(i) x=20より、10.4秒 (ii) x=0より、11.0秒
b 最短時間はx=8のとき、9.8秒

<海外の反応>
社会に出ても常識ない奴が多いのに、こんな99%の人間に必要のない高等数学を教えて何したいんだろうな。あいつらにはもっと税金とか住宅ローンのことを教えてやってくれ。
え、普通に解けたんだが・・。最近の学生はこれぐらいでワーワー言ってんの?
残念だが、ワニもシマウマもアメリカ人歯科医に撃たれるから答えは永遠に出ないよ!
簡単すぎwwwwwwごめん、嘘です。
シマウマさんは全力で逃げるだろうし、だとすればこれに何の意味があるんだよwww
本当ふざけた問題だよなー学生もこんなの習ってどうすんの?










コメント
コメント一覧 (87件)
普通にXに代入していくと解ける
授業を聞いて理解していれば分かるはずなんだが
最初が地上を移動しないX=20 次がX=0
最後に代入式+4を変形して
式(x)-4=0となるように計算していく
ずっと水中を行けば最短距離を速く泳げる水中で行けるのに、何で途中で陸地に上がった方が速い事になるのか訳が分からなかったが、やっと理解した。
これワニが水中より陸地の方が速い設定になってるね。
*1さん、
私は数IIIの微積で解いたけど、
あなたのが分からん。
もしかしたら微積なしで解けるんですか。(16歳のテストって言ってたから確かに16歳には無理だなと思った)
え、これ中学生レベルの問題じゃないん?
全世界でゆとり化進行してるん?
普通に図に書き直して考えたら凄い簡単なのに・・・
アグネスは、金になら無い話に興味は在りません
世界の子供のために募金宜しく
※1
うん、そうなんだけど、これはいい問題だよね
この年代の家庭教師してた時に、文章題に躓く子が多かった
やはり国語力は数学にも必要だよね
俺は先ずキーワードを書き出せって言ってたけど、この問題は、式に惑わされるかどうかw
式としては難しくないんだが、獲物に忍び寄る速度とかに使う式じゃないよな
電車とか機械装置を例にした問題に使うべき
※6 追加
森博嗣さんの小説で、入学試験の問題の難易度の話があったけど
難しすぎるって却下されたが、ふるい落とすための試験である以上
問題の解法に気付くような頭が柔軟で優秀な生徒が欲しいって趣旨だった
あれは納得したな、この英国の問題もいい問題だと思うよ
気付けば簡単に解けるんだし
式の意味を考えると第1項は斜めに水中を進む時間(速度x距離)で
第2項は陸上の時間を意味してる。
水中対陸上では5対4で水中の方が時間が掛かる。
この問題を解ける16歳は0.02%以下じゃないかな。
T(20)=104からして計算機+四捨五入だな
それともイギリスだと根号を外す計算を普通に使っているのか
それともあたりをつけて前後計算しているのか・・・
bの方は微分を使わない方法があるなら教えてくれ>※1※6
普通「川幅は6mです。」
みたいな条件出して、自分で式を作らせるところを
いきなり式出して思考停止させるイジワル。
式を冷静に見たら単に水中でかかる時間と陸上でかかる時間が表されてるだけで
川幅が6mということも分かる。
式があるなら代入するだけだろ
やっと理解できたorz
速さが4:5で川幅が6mだからx:√(36+x^2)=4:5になればいいのか
って自分で理解できても人に分かるように説明できてないな
ややこしすぎる
あらやだ、解けちゃった。
シマウマの生息地域にワニいるものなん?
いい問題だと思います。必要な知識は中二で十分だし。
ただこれが1問目にあったらヤダ
真上から見た図で出題すべきだろこれ
ワニからシマウマまでの実距離とワニから垂線の足引いてその向こう岸からシマウマまでの距離とを混同して見てしまったじゃないか
ワニとかシマウマだと思うから難しい
最初問題の意味がわからんかったけど問題文が若干おかしいなこれ
素直に読むとT(x)の式のxは最短時間になるための距離ってことになるからこれにx=0、20を代入するのはおかしいってことになる
あと※1の人は解答部分見たんだろうけどたぶん理解できてないんじゃないかな
解答例では※3の言うとおり微分使ってる
16歳の問題ってことだから微分使わない方法があると思って考えてたんだが解答例で使ってて拍子抜けした
コメにもあるが、ワニが全速で陸上を12mも走ればシマウマは逃げおおせるだろう
最適化問題?
ん?微分して極値を求めて正解には辿り着いたけど、>>13とか微分を使わないでも同じ式にはなるな。
なぜだ?説明求む。
bを微分使って解いた俺は16歳の時点では解けなかっただろうな
式が表す意味とか分からないあたりが文系の限界か…
これはもとの式に平方根があるからたじろぐ人がいるかもしれないけど、考え方は難しくない
微分を使わない解法、なんかわかったかも。
入射角のサインが速度比の屈折と考えればいいのか。
※25
俺もそれは思った
光路差の話と近い
たぶんフェルマーの原理とか調べるとはかどる
うーん、つまり三平方の定理って奴だな!?
微分使っていいなら全問解けたが、日本の制度下の16歳には最後の問題はキツイと思われる。
イギリスやアメリカなどは,大学入試に相当する資格試験で,グラフ電卓や科学電卓の利用が当然のこととなっています.
向こうは根乗電卓使えるらしい…
そうなるとクッソ簡単だよな
俺の頭では微分以外で回答に導けない。自分頭悪いっすわ。柔軟な思考がないからかも。あとで息子に出してみるわ。
数式見た瞬間、脳が拒否した
※欄のみんなすごいな。いや、私が馬鹿なだけなんだろうけど
もし、水中での式が右辺左の5√(36+x^2)で表され、
地上での式が右辺右の4(20-x)で表されているのなら、
これら2つの式の交点を求めればできるんじゃないの?
って思って計算したら答えが合わない。
なんで?何か考え方おかしい?
誰か教えて!
octave:1> q=@(x)5.*sqrt(36.+x.^2).+4.*(20.-x)
octave:2> x=0:0.1:20;
octave:3> plot(x, q(x));
octave:4> fminsearch(q, [0])
ans = 8
おとなになるってかなしいことなの……。
(本当にこれ、16歳用ですか…?)
※33
SQAは16歳でスタンダードグレードを受ける
で、大学を目指す奴らが17歳でハイヤーグレードを受ける
原文の記事を見るとこの問題はthe Higher Maths examってなってるから
実際は大学進学を目指してる17歳が受けるやつじゃないかな?
ねえ みんな何の話してるの?
文系出で今30の俺だけど、既にルート使った計算ほぼ覚えてないよ
あの学生で使った時間はほぼ無駄だったよ。
職業的に一番勉強しなかった国語と古文、英語しか役にたってね・・・・・・
※32 戸外団かな?
問題文みてシマウマ逃げねーのかよ!あと川幅いくらだよ!って思ってしまった
米38
式に川幅と地上・水中の速度は記載されてる
5√(36+x^2)+4(20-x)って事は
川幅が6m(=√(36))
水中の速度が秒速2m(×5→÷1/5、時間単位が1/10秒なので10倍する)
陸上の速度が秒速2.5m(同上)
って事だ
ワニ水中より陸上のが早いとか、先入観も罠になるなw
追記
速度の×5を÷1/5に直したのは
移動時間=距離÷速度 だからな?
速度を逆数にして掛けてあったって罠だなw
文章に載ってない数字を式から拾う能力があれば(a)は回答できる
(b)はさらにxを求める式に変換できれば求められる
ワニだシマウマだってのはある意味余計な情報だわな
水陸両用メカとゴール地点として読めば良い
平方根と代入式を理解していることが前提
36という数字が6の2乗と分かれば、5*式+4*式の合計が時間
4*が20-xとなりこれが陸上距離
5*平方根式が水中距離
最後にxを求める
微分を使わないと求められないと考える、頭の固い人には柔軟?でもなんでもない単純な定理が理解できない
平方根と代入がなければ中学受験で出るレベル
点と点の間の移動という単純なシチュエーションに置き換えたら解けた
ワニとシマウマにかなり意識持って行かれたわ
>>40
>(b)はさらにxを求める式に変換できれば求められる
>>41
>最後にxを求める
いや「微分使わないとできなかった」って言ってる奴らはまさにその部分の論証が気になってるんだけど
(a)の説明なんてされずともわかってるから(b)の細かい解答を教えてくれよたのむよ
屈折の法則使って無理矢理求める方法なら思いついたけどそれ物理の範疇だし
解けたヤツが合格
解けなかったヤツが不合格
って単純な話
解けたヤツが0人って
言うなら別だがな
俺なら問bはxを整数と勝手に決めうちして1から19まで代入してただろうw
aは流石に分かる、いい問題だと感じるのは自分が学生じゃないからなのかな
(b)は上流20mでも100mでも同じだよね。
要するに角度のサインが速度比になるってことを覚えておけば微分は使わない。
でも、なぜそうなるのか>>13様、ヒントをくだされ。
みんなわからないなら影響無いやん
※41「最後にxをもとめる」ってさらっと書いてごまかしてるけどそこで微分使わなきゃいけないんだけど^^;
f(x)=0のような方程式問題と勘違いしてるんじゃないかな
f(x)の最小値を求める問題だから微分が基本
フェルマーの原理とかの光学系についてちょっと調べてみたけど変分原理(微分の親戚みたいなやつ)を用いて示されてるのしかなかったから頭の柔軟さでどうにかなる解法はおそらく無い
あるなら教えてくれ
T – 4(20 – x) =√・・・ と変形して両辺二乗すると、
Tを係数に含むxの二次方程式ができるので、(a)の範囲でxが
実数解になるような最小のTを判別式で求めた。微分も光学も
使わない方法で解けたけれども計算が酷く大変。
※50計算がめんどくさすぎて途中で投げたけど理屈としてはこれは出来そうだな
陸上移動の方に奥行きが無くて真横移動だから光学よりすこし問題がシンプルなんだな
どちらにせよ中学の指導要領じゃない気もするが・・・外国では中学でここら辺習うもんなのかね
9.78じゃないの?なんで9.8?
この計算でいうとシマウマが上流8m地点にいた場合、ワニは常に水中を移動するのが最速になる。
ものすごい違和感があるのだが・・・
xを大きくしていくと陸上を進む距離が短くて済むが水中を進む距離が増える。
問題式の意味から川幅6m。速度は陸上:水中=5:4。
よって斜めに泳いだ水中を進む場合√(x^2 + 6) – 6 だけ水中の距離が増える。
一方が増え、一方が減る。両者が一致した地点が最少時間になる。
計算では時間=距離x速度で行う。
Xが無限だと陸を歩いても泳いでも回答が同じになる
>>54
めちゃくちゃでんがな。とりあえず式で解答まで表わしてみて。
4x = 5(√(x^2 + 6) – 6)
この式を計算すれば答え。計算はめんどうなのでしない。
※57どういう経緯でこの式が出てくるのかわからんが不正解ってことだけはわかるわ
√(x^2 + 6)なんて項がでてくるはずがないし
あと※54の最後の2行だけで大量に間違いがあって何がなんだか
追記※53について
確かに違和感あるけど「シマウマが上流8m地点にいた場合、ワニは常に水中を移動するのが最速になる」よ
微分の解法見れば分かるけど20mの部分は微分で落ちるからシマウマがどこにいようがx=8が答え(上流8m未満にいた場合は除く)
どうでもいいけど川の幅について言及されてないから問題として微妙じゃね?
※59と思ったが式の意味考えればわかるのか、納得
>>58 訂正する。
4x = 5(√(x^2 + 36) – 6)
x = 0 だと 6mを水中を最短で陸へ移動して直角に曲がり陸を移動。
x > 0 は斜で距離は(√(x^2 + 36)だが川幅6mを差し引いた分だけ距離が増える。
増えた距離の分時間が余計に掛かる。
陸はxだけ距離が減る。
xを大きくしていくと陸での時間は減るが水中での時間が増える。
陸で減った時間と水中で増えた時間が一致した所が最少時間。
速度の差陸5:水中4を加味して式を作ると上記式になる。
>>61
x=8が最速だからどっちにしろ間違ってるし
距離に速さかけてる時点でもう小学校からやり直してこいって感じだし
流石に釣りだよね?
※61
解がx=8なのは既知なわけだが4x = 5(√(x^2 + 36) – 6)はそれを満たしてないからだめだな
理屈的にも「陸で減った時間と水中で増えた時間が一致」っていうのは全てのxにおいて満たすべき条件であってT(x)の最低値を求めるための条件にはなりえない
>>62,63 間違ってた。まず速度4と5が逆になってるし、
>>63 の言うように減少分と増加分が等しいというのが間違ってた。
国語の問題のような気がしてならない。
5x=4√(x^2+36) がxを求める正しい式なんだよ。微分すればわかる。
ただ、これは>>13が気づいたようにx:√(36+x^2)=4:5 であることに気づけば
微分を使わずに求められる。
>>13 はわかっていないんじゃないか?
そうか。そもそもスネルの法則も合成微分を使わないと証明出来ないから、法則を知っていれば微分使わないで解けるってのも意味ないか。
ずいぶん速く動くワニだなw
この河は流れてはいないのか。
問題を理解するのに数分掛かったわ
理解すれば問1は代入するだけだし問2は後回しして良い範囲かな
T(1/10秒)ってのは何の意地悪だ?
※ただしこの川には魔物が潜んでいるものとする
これって英文の問題の出し方が難しかったのでは?
あと水中のワニは二足歩行している
合成微分を知っていれば瞬殺レベルのサービス問題だな。
で、合成微分は文系も理系も高校2年で習うんだっけか?
図がおかしい
それに尽きる
微分しない正解は※50の計算なんだろうけど、
※13?の考え方も的を得ていて、ようは二次関数の極値なんでそこからΔx足したり引いたりしてみて差が出たらいかんでしょって思いまーす。
※50 だけれども、相似と三平方だけでも解けた。解けてしまうと最初の解法(判別式)の醜いことこの上ない。
相似のヒントで俺もわかった。対称点をとって直線で結ぶんだな。
す、数が苦…
現高2、16歳のものです。
ほとんど同じ問題が期末試験にありましたが、できました
普通に数3微積分の速度と近似で扱う範囲ですし、問題集なんかに普通にでてきますよ笑笑
というか、進学校に通う人、もちろん国立志望の人は少なくとも高2で扱うわけですし、さほど難しくないですよ、、、
入試中級レベルのもので、確かに16歳では応用的な問題ですが、紛糾するほどではないです笑
大学の知識いらないわけだし、検定範囲内の、特殊な考え方もいらない問題なので笑笑笑
T(x)=√(3^2+4^2)√(6^2+x^2) + 4(20-x)
って変形したらコーシーシュワルツで一発じゃん
あほくさ
”ワニの問題”に 漂着した;
http://yurukuyaru.com/archives/45103984.html
この問題に終結符をつけたいのか
XJAN が ↓の如く 終結式 を 持ち出し解いた;
http://userdisk.webry.biglobe.ne.jp/020/691/47/N000/000/006/148612079734346187180.gif
XJAPAN の かいとう を 解説願います(コメントランを覗き見して)
^^^^^^^^^^^^^^^^^^^^^^^^^^^^
>83
T(x)=yと置いて、与式を変形すると、9x^2-8xy+640x-y^2+160y-5500=0
この格子点を求めると、(-8,62),(-8,162),(0,50),(0,110),(8,-2),(8,98)で、0≦x≦20,y≧0でyの最小値はy=98
つまり、T(x)の最小値は98より9.8秒。しかし、xもT(x)も整数とは限らないのでダメですね。
解答としては46番さんの方がいいですね。
ちなみに、xもT(x)も整数と分かっているなら、√(36+x^2)=aと置いて36=a^2-x^2 ∴36=(a-x)(a+x) a-xとa+xの偶奇は一致してa+x>a-xより、(a-x,a+x)=(2,18)のみ。∴a=10,x=8
∴T(x)=50+48=98 ∴9.8秒
※82
やるじゃねーか。16歳がシュワルツの不等式を知ってるかはさておいて、割と感動した
微分すればできるだろ
微分禁止だっつーの。日本の中学入試の算数みたいな発想を要求する問題だね。