
オーストラリアのビクトリア州統一試験(VCE)で出題された数学の問題が、あまりにもレベルの高い難問だとしてネット上で激しい論争を呼んでいます。求めるのは隣り合った50セント硬貨の間にできた角度。
Year12(17~18歳程度)の高校生らが阿鼻叫喚した問題、みなさんには解けますか?
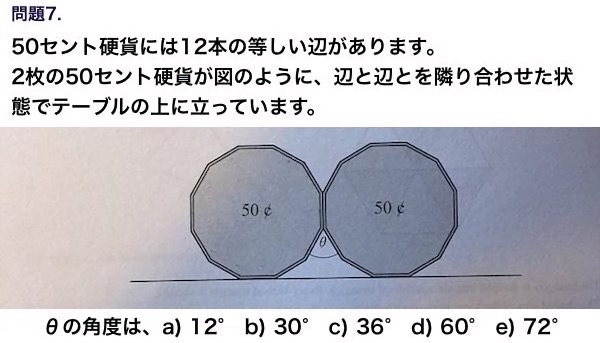
こちらが激ムズな高校数学の問題
<学生たちの怒りの声>
50セント硬貨の角度を求める問題だけど、私には全く理解できなかった。だって他の角度も辺の長さも書いてないのよ?これだと公式に入れられないし、どうすることも出来ないでしょ!
50セントはくたばりやがれ!てめぇの音楽もどうせ嫌いだったし!!
この試験は学生をテストするためのものじゃなかったよな。あれは騙しだわ。こんな問題、誰も準備出来てなかっただろw
マジでふざけんなって感じだった。
こんなのが実生活で役に立つのかよ?あぁん!?
何度になるか、いまだに考えてるんだが・・
5つの選択肢から回答を選ぶものでしたが、多くの学生がこれに悪戦苦闘。不満をネットにぶつけているものの、傷口に塩を塗られるというのはこのことでしょうか。ネット民の中には「難しすぎる」という感想に疑問を投げかける者もいます。
こちらが実際の問題用紙
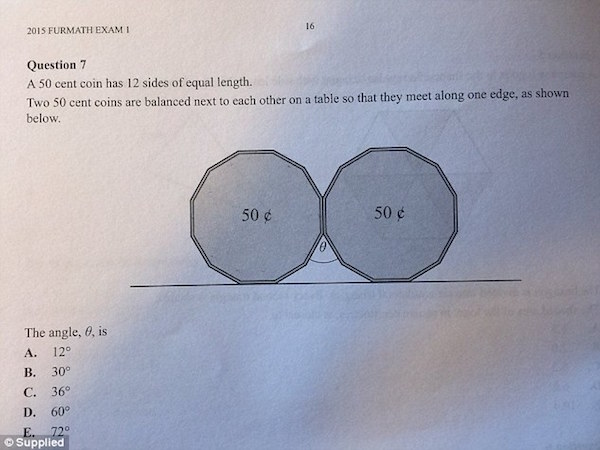
解答:
60°
解法例:
多角形の外角の和は360°なので、ひとつの外角は360°÷12=30°
ここでは2つの外角が隣り合っているので、2倍の60°となる
他にも、内角の和から求めることも可能ですね

<海外の反応>
ガキが何喚いてんだ?数秒もかからなかったぞwwwww
やっべ・・見ただけで答えが解ってしまったわ。これ常識レベルでは?
スポーツ選手、俳優、ポップスター、セレブなんかを尊敬する文化を作り出してるから、こんな問題もろくに解けないんだと思うわ。
なんでだろう。これ解けないって言ってる人は考えすぎなのかも。
いやでも、これが難しいって感じる学生がいるんだし。これは数学教師の問題だと思うよ。
12歳の問題の間違いだろ・・
問題が難しいからブチ切れてるんじゃなくて、勉強できないからブチ切れるしかないんでしょうね。めげずに頑張って欲しいですが。













コメント
コメント一覧 (119件)
小学生のための問題だろ
びっくりした
確かに何が難しいのかわからんな
問題文3回見直したわ
ああ、やっぱりな。俺もオーストラリア人がアメリカに留学していた時に、
180$の買い物で俺が200$を渡して、20$札のお釣りをもらっていたら、
「どうやったんだ? どうして奇麗に20$札1枚をお釣りにしたんだ?
小銭なしで札1枚にするなんて、アジア人は頭いいな」と言ってきて、
こいつらマジで計算以前に頭おかしいなと思った
見た目でも60度とわかるだろ…これ
計算が必要なら難しいけど、選択問題だから見ただけで分かる易門じゃないか
えっ。糞簡単じゃね?
いくらなんでも、頭悪すぎ・・・www
着眼点がずれるとハマりやすい人は居るからねぇ・・・。
つかこれ選択問題かw
なんだ、マジでそんなに難しいの?
って見たら……何か引っかけじゃねぇの?って探してしまったよw
日本人ってやっぱり優秀なんだねw
難しかったとして、他の受験生も同じ問題をやるんだから条件も同じ。
あんまり簡単だと、高得点ばかりになって受験生どうしで差がつきにくい。ちょっとしたケアレスミスのほうが数学の理解度より合否に大きく影響するようじゃ、そのほうが不公平ってもんじゃないかな。
なんかのひっかけかと思った。
たしか中二の教科書にこんなのあったんで小学生レベルではない。
でも小学生でも解けそう。
これはツリだよね??
小学生レベルなんだけど…
見た目も結構なヒントになるなこれ。
自分もひっかけかなにかと勘ぐってしまった。
この硬貨、スゲー重たくてガサるのな
お釣りで貰うとゲンナリするんよ
公式に当てはめられないってコメントから、
そう言う教育しかしてないのだと思う。
形にならないと対応出来ないみたい。
NZの話だけどあの辺の奴らは本当に計算ができない
屋台で1個2ドルのホットドッグのA味を2つ、B味を2つ頼んだら
オーダーは通って(言葉は通じて)ホットドッグを4つ渡されたけど「4ドル」って言われた
多めに請求されたならボッタクリかもと思うけどさ、まああんなんでよく商売ができるなと
解けて、よかった
確かに、角度が誤摩化してないから、見ただけで解けるwww
数式にしたいなら、内角の和が360度180度ってやっていく所から書けば、点数貰えるんじゃ無かろうか
一応中学校レベルの問題だけど、頭の良い小学生にも解けるかもね
難しいって言われると、かえって考えこんでしまうだろな
何も考えずパッと見れば一瞬で解けるw
文系の俺
外角の和から答えに辿り着いたが
内角の和からは分からないもよう
塾講やってて中学生に教えてるから一瞬でわかったわw
どんな難問なのか期待して開いた自分がアホだった
引っ掛け問題かと思った・・・。しかも選択問題じゃんかwあてろやw
見た目で判断せず講師気を使わずとも
12辺あるから30度の鋭角三角形に分けていって……と気合で計算したとしても暗算でできる
>>20
(n-2)x180/n
nに12を代入
(12-2)x180/12=150
ちなみに俺も文系
中学生には簡単過ぎる、もし50セントではなく正12角形って書いてあったら小学生でも解ける
日本の学生なら大丈夫だと信じたいな
分度器を持っていた俺に死角は無かった
※3
それは合計180ドルぴったりになった事が凄いと言う意味では?
175ドル45セントじゃなくて、みたいな
え、問題文呼んでる途中で絵を見たら答え出て来ちゃうんだけど
水平の辺が垂直になるのに3回角度を変えてるから30度の変化
それが二倍で60度、どこに公式とか必要なのかと
※28
そんな考えもあるのね。
私は二等辺三角形の角度から出したわ。
正多角形の内角/外角の和って、今小学校で教えないんだっけ?
公式を習わんでも自力で導けると思うけど。
自力で公式も導き出すなら、内角を利用するほうがちょっとだけ難易度が低いかな。
どっちにせよ小学生が普通に解ける問題だが。
やべえw
360÷12で30は出したけど倍にしなかったw
…同列かやだな
えぇ・・・・簡単すぎるでしょw
360を12で割って×2するだけじゃんw
内角/外角の和の存在は忘れてたけど少なくとも
360度/12=って式ぐらいは思いつくだろ。
オーストラリアだぞ馬鹿ばっかのw
全然驚かねーわw
(360/12)*2
呆れた。
こんな簡単な問題は高校入試でも出ねえぞ・・・
本気で中学生レベルだとは思わなかった……
高校生でこれが難問とか言ってたらマジにやばいな
角度が書いてないから無理とかいうけど、角度が書いてあったら問題にならんだろこれwww
これ日本なら小学5年生でも大半が正解すると思う。
解き方を知ってるか知らないかだけだから
次に解ければ問題ないで(*´ω`)
ただ角度を出すだけなら暗算で5秒未満だった
一周で360°変化するんだもんね。
(360/12)×2
証明も記述しなければならない場合は、違うやり方事を書くと思う。
例えば→(途中略)→最後に360-75×4とか
にしても頭の中なら10秒未満
日本なら正解率の高い中学生用の問題かな
>>4
おまえはオージーと同じぐらいバカだ
シンガポール、日本だと学校のレベルによる
しかし、大学になると基本勉強漬けじゃないと卒業できない欧米と逆転する
東大卒の将来を嘱望されてた旧財務官僚が米に留学して高等数学が理解できず留年、帰国したことがある
見りゃ解るだろというレベルではあるな…
気の利いた奴なら小学校でも解けそうだ
内角外角の公式は忘れたから二等辺三角形を使って答えを求めたけど、三角形を用いた角度計算問題としても難易度的には普通か少し易しいぐらいの問題だよね。
>>43
おまえは朝鮮人と同じぐらいバカ
60だろ?
オーストラリアって馬鹿www
証明のいらない選択問題なんだから実測すればイイジャン
って分度器がないと60度が分からないと。
その程度の問題なんでしょ。
※43
選択問題なんだし、※4 も短い時間で点数取る為のテクニックという頭の柔軟性は必要だよ。
数学に限らず問題を解いた結果と直感的な推測とが合わない場合はもう一回見直ししたほうが良い。
内角の和から求めたワイ無事死亡
外角の和とか全くおぼえてないわ
360÷12×2で小学5年くらいの問題
30年くらい前にも豪との交換留学生の手記を読んだけど
やっぱ英語やほかダメダメになったけど、数学だけは学校でトップになったって話あったなぁ。
この子もアホなうえに浅はかなんだろうけど、学力・進行度は今もって格差があるらしいなぁ。
これが解けない高校生がいることの方が驚きだわww
選択問題なんだからdかeかで適当でええやん
え?暗算で出せるんだけど?
50セント(ラッパー)、名前のせいで、とばっちりw
※51
覚えてるも何も一周が360度なのは常識だと思うんだが・・・
おそらくその常識をちゃんと活用できない状態ってのがオーストラリアレベルなんだろうな
中学の問題かと思った
高校なのか
こういう角度求める問題いっぱいやらされたなー
どれくらい難しい問題なのか期待した私がバカでした。
てか他の問題はどれくらい簡単なのか気になってきたわw
接地面を1辺目とした時、3辺目で90度になり、両方のコインが接している。
また、隣り合った各辺同士の角度は等しいので、その外角も等しい。
よって外角1つあたりは90/3=30度、求める角度はコイン同士が接触している辺から
1外角分が左右合わさっているので30*2=60度
計算して45度の直角二等辺三角形を見つけたらすぐ求まるなぁ
こんな中学生レベルの問題でいちゃもんつけられるなんて
数学教師って大変だな
いや日本人もいまの高校生ぐらいでこの問題解けないやつ結構いると思うよ。
平均的な数学の学力かなり下がってるし
分からんかったっす
どんなひねった難問かと思ったら小学生レベルで草
パッと答えは出なかったけど角度の和で求められるんじゃね?って普通に思った
こういう問題の解き方を教わってないんだろ
日本のカリキュラムではありえんけど
馬鹿にしてる奴は国に感謝しろよ
シータ角とすぐ下の両コインの鈍角2つ、この3つを繋ぐと正三角形になるんだわ
360°を12で割れば硬貨を12で割った二等辺三角形の角度が出る。
75°*2-180で外角出して、それを二倍にしたら解が求められる。
解き方とか多角形の外角の和とか完全に忘れてたから全く別の方法で出したわ。
発想力があれば小学生でも解けるな。
これは簡単すぎるだろ……
辺の長さは必要ないし、逆にどの点で難しいと思うのか聞きたいぐらいだよ
仕方ないよ文字覚えたのも最近の連中
教育自体も真面目に受けないバーバリアンwww
θ = (360 ÷ 12) × 2
= 360 ÷ 6
= 60
暗算レベルの超簡単な問題ですやん
そもそもオージーは円が360度という事を知らなかったり?
あえて釣られるのもアホらしいけど
高卒の30歳だが5秒で解き方は分かったし計算を含めても30秒かからなかった
もう計算の仕方も忘れた
これ見ただけでなんとなく60度ってわかるが
回答の選択が61度、63度とかならわかりにくいのにな
正確な作図すぎてひと目でわかるなw
解き方と言ってる奴は数学的センスなし
難しいって前振りで問題を見てしまったもんだから、逆にこんなオーソドックスな問題じゃないはず!って、現実逃避しちゃったじゃないかw
学校によってはこんな問題も出るだろう
ここで俺sugee、こいつら馬鹿かよって言ってる奴は、偏差値28の奴なら解けなくて当たり前って事も考慮しろよな
※9
日本人が優秀なんじゃなくてオージーの頭がおかしいだけだろ
小学生レベルの問題じゃねぇかwww
日本だと小学生レベルの問題だな
一回見ただけでわかったんだけど、、、オーストラリアの中学生は円が360って知らないのかな。
「こんなん簡単ww」
問.50セントは何ジンバブエドル?
「ヒ、ヒィ~~」
数値出すのはめんどくさいからしなかったけど、2倍ってことはわかった
倍にするの忘れた
子供の頃から図形問題苦手だったから外角ってなんだっけ?ってレベルだけど、
対角線引いて三角形作れば私でも解ける問題じゃないか
こんなので解らない言ってるような奴らより日本はGDPやら年収やら低いんだぜw
笑ってまうわwwwwwwwwwwww
>3
嘘やろ〜?
180ドルの買い物に200ドル渡したら、チップ込みと思われて『Thank you!』って言って終わるんがアメリカさんやんか。
釣り(^^)
算数や数学を完全に忘れてるおっさんでも簡単に解けたぞw
いや、今の中2なら簡単じゃないか??
2分くらいかかってしまった…
12角形の内角の和が1800だから
一つの内角は150度
360-150-150で60度
この生徒はドツボにはまって出られなくなっただけだろ
公式うんぬん言わずに補助線を引くなりすれば解けたとおもうよ
証明しろって言われると困るけどなw
360°を均等に12分割してるとは限らないわけでw
選択式なら楽勝。
どれほど難しいのかと思って覗いてみたら、中学受験のしかも偏差値低めのところででるのかすら怪しいボーナス問題じゃないか。
>>98
角度も等しいとは宣言されてないから正確な定義としてはちょっと怪しいけど12本の等しい辺と言ってるからそれで正12角形として判断していいんじゃね
学生時代に余り頭良くない学校内の、しかも学年最下位常連の学力だったその自分ですら一瞬で解ったのに、外国人は何を阿鼻叫喚しとるんじゃ!
ホームステイ先の大学生の教科書、化学記号覚えるだったときが衝撃・・・高校化学じゃモル計算とか
やらないそうだ。今もたぶんやってない。
すぐ出たけど360°の和を忘れてたので、多角形中心点を通る水平線を底辺とした直角三角形で出したわ
180-(90+15)=75
180-(75×2)=30
θ=30×2=60
実際解いてないけどなんとなく60だと思った
人としてダメだな
外角の和ね・・・もう忘れたw
二つの50セントの上に接するようにもう一つの50セントを置くと、正三角形ができる。よって180÷3=60となる。
三角形の角度の総和が180と習うのは今の日本の学習指導要領だと小学四年生である。いくら指導要領の違う国とはいえ小4レベルの問題を高校生が解けないとはいかなるものか。
これ選択問題かよ
中学もしくは高校受験レベルだろうに
俺灘高生、爆笑
こんな奴らにイエローモンキーって見下されている事にイライラするんだが
こんなん小4の時に解けたわ
中2の範囲かな。
中間テストで普通に出るだろ
公立高校入試に出たらこんなのサービス問題だろう
何がどう難しいのかさっぱり分からない件
公式に当てはめるだけの問題だが
オーストラリアでは公式とか教えてもらえないの?
アメリカの大学”院”共通試験であるGREの数学の問題(Generalの方)見てみたらいいよ。簡単すぎて笑えるから。
※8 灘高生は英語圏の知識が浅いと笑われるから黙った方がいいよ君。。それ教えたの年配の方でしょ。。
見た目で隙間が正三角形w
日本人なら一瞥くれて60にマークして次の問題w
みんなそんな簡単に解いてるのかw
360/12=30
180-30=150
360-150*2=60
ワイめんどくさすぎwwww
冷静に考えればわかる。
※33
360出てきてる時点で多角形の外角の和知ってる前提じゃねぇか
低レベルな問題で俺sugeeeeeしようとすんなよ低脳
小学生からやり直した方がいいレベルのアホがいるな
コメント欄読む限り本当に頭いい奴なんて一人もいないな
まあ政治見れば日本人の頭の良し悪しがはっきり反映されてるわけだが
50セントディスられて草