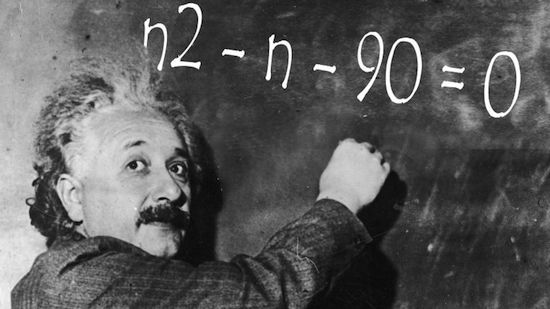
イギリスでは4日、GCSEと呼ばれる全国統一試験が行われました。
義務教育が修了した16歳(日本でいう高校1年生)が受験するテストなのですが、そこで出題されたある数学の問題が「超難解だ」として、ツイッターには怒り・絶望の声が集結。トレンド化しています。
こちらが、16歳が絶望した数学の問題。
バッグの中にn個のアメ玉がはいっています。
そのうち6個はオレンジ色です。
残りのアメは全て黄色です。ハンナちゃんは、バッグから無作為にアメを1個取り出し食べました。
そのあと彼女はもう1個、無作為にアメを取り出して食べました。
ハンナちゃんがオレンジ色のアメ玉を2個食べる確率は3分の1です。
(1)n^2 – n – 90 = 0 が成り立つことを証明せよ。
この問題を読んだ高校生の多くは思考停止。
英BBCの取材に応じた学生の中には「意味がわからない。これを出題した人は私たちにアインシュタインになれっていうの!?」「ハンナにはマジで泣きたくなった」「この問題が分からなくて、試験会場で実際に泣き出している人がいた」などのコメントが。
そしてこの数学の試験後、なんと20万人にものぼる人がツイート!
問題の難しさも相まってか、ツイッター上では「#EdexcelMaths」のハッシュタグでトレンド化しています。
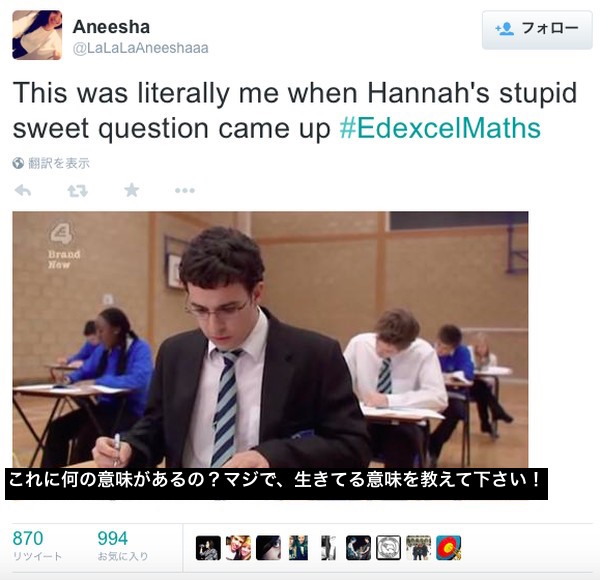
試験問題前半にとりかかる私と、後半(ハンナ)にきた時の私
「(前半に出題された)問題」vs「n2-n-90=0」
ハンナのアメ玉の問題が来た時の私
ハンナはケツの穴にアメ玉ブチ込めばいい
みなさんは解けましたでしょうか?こちらでは考え方だけ載せておきます。
1個目のアメがオレンジ色である確率はn分の6、2個目のアメもオレンジである確率は(n-1)分の5。これらが同時に起こる確率は乗算で求められるので、
6/n x 5/(n-1)=1/3
30/(n^2-n)=1/3
n^2-n-90=0
Q.E.D
ハンナの馬鹿げたアメの問題が出てきた時の私
今日の数学のテスト
オーマイガー!
[@eleanormay__さん]
全国の16歳が疑念と憎しみで団結してる姿がイイネ

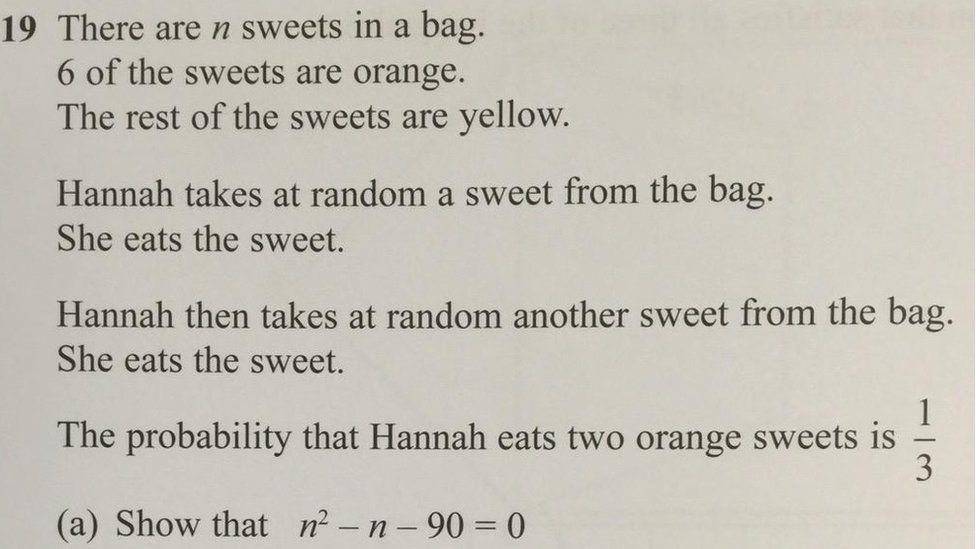



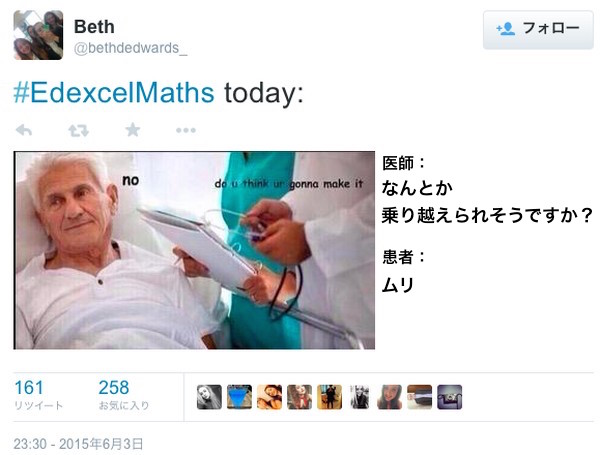









コメント
コメント一覧 (139件)
簡単すぎる
あー、そうそう、これで合ってるよ、OK
って書けばいいんじゃない?
これ、ネタか?
日本の高校生なら難なく解きそうな問題だと思う
日本の公立高校入試に出てきてもおかしくないような問題だな。(文章の形式は違えど)
内容としては中2レベルだし
まだ習ってないとか…そういうことなん?
えーと…普通に解けたけど…何が難しいのこれ。
問題文で惑わす意地悪な問題だな。
実際はアメ玉の数を求める計算式でしかないのだが、パッと見は謎の計算式に見えてしまう。
「オレンジ玉2連続の確率は1/3です。アメ玉は何個入っていたのでしょう?」
という問題なら多くの人が解けたと思う。
いや流石にできるんじゃねぇかなこれは…
あまりこういう問題見たことないから戸惑うかもしれんが落ち着いてみれば普通の確率の問題じゃん
イギリス人は数学が苦手なのかな(´・_・`)
中学生レベル
中学受験する小学生でも解ける
うーん。数学の問題だけど読解力を試されているとか?
※8
いや、全然。
それ、典型的な問題文から関係式を起こせない子の思考回路だよ。
論理的に文章が読めないから、得てして他教科の成績も悪い。
つうかいかにもアインシュタインが嫌がりそうな問題だなw
アインシュタインはドイツでは落第して大学進学できず、スイスの大学に浪人して入ったような人
こういったただ困らせて落とすことが目的の問題は苦手だっただろう
これは普通の中学生なら誰でも解けるんじゃねーか?
複雑な問題じゃないからなぁ
ていうか中学入試でもっと難しい問題が出るよね
中学入試レベルでしょこれ
問題文がふざけてるって事でいいのかな?
16歳ってことは解答者は中卒レベルではあるんだろ?
こんなんで思考停止ってレベル低すぎ
(6/x)+(5/(x-1))=1/3
これの解を求めるだけじゃないのか?
これは大問19の問(a)の証明問題でこの後に(a)証明を応用した問題があるんじゃないのかな?
大学入試なんかでよくある感じ
肌色のハンナちゃんprpr
ハンナちゃんにいたずらしたい
IQテストで本気出せないみたいな話か
クソ簡単やないかい
分数式が絡むから一応高校2年レベルだろ(数学Ⅱ)
中学レベルとか言ってる奴らは証明途中の分母の扱いで減点を食らったりしそう
へ?余裕だよね。というか、1/3になるという設定が問題としてレベルが低いよね。
ベッカムも算数出来ないしw
条件から、普通に方程式を立てて、変形すればすぐでるぞ?
それに、証明する式の形からも推測できるぞ。
確率は、ちゃんと区別しないとダメなんだよな。
このあと、整数問題でnを求めさせそうだな。
直観的にアメ玉10個ってわかっちゃった。
中学の問題ではないと思うけど、この分数式なら数学Ⅰじゃないの?
イギリス中のハンナさんたちは無事なの?
日本なら中学で習うから、少なくとも半数の中学生は解けると思う。
結論、馬鹿外人大杉
揚げ足取りで申し訳ないが、誰も指摘しないので
※19が間違っている件を報告
フェルマーレベルの問題でも出たのかと思って、驚くべき証明を見つけたがそれを書くには余白が狭すぎる、とか書こうかと思ったが、普通の中学生問題だった
※35
誤 +
正 ×
ちなみに、東大で出題された
「円周率が3.05より大きいことを証明せよ。」
って問題、イギリス人ならなんていうんだろ?
※14
アインシュタインは数学の成績は良かったよ
ま、でも特殊相対性理論くらいなら、大した数学は要らない
取り敢えずお前らは問題を解いてろ。
ハンナちゃんは俺が面倒をみてるから。
さあ、ハンナちゃん。
お兄さんとペロペロしようか。
書かれてることを
数式に変換しなさい
て事だよね。
イギリス人は英語が苦手なんだろ
あータイトルには高校生ってあるけど実質中学生か……
中学生ならできない子がいても不思議じゃないやろ
しかしキレ方がイギリスっぽくて面白いな
nが何個かという問いなら解けるのだろう
その途中式が成り立つことの証明となると普通やらない
※39
そのきたねー飴玉をひっこめな
文章通りに式たてれば普通に解ける。
入試問題ならもっと難しい問題とかあるよね。
日大でセンター1aが60点しか取れない俺でも解けたのに・・・イギリスで受験したかった
なんか数学って言うより読解力の試験してみるみたいだ
整数解を持つ飴玉の個数がない件について。
飴玉は砕いたのが入っていたんだろうか。
少し悪問かな めっちゃ簡単だけど習いたてだと知識がでにくいかもね
バッグの中にn個のアメ玉がはいっています。
そのうち6個はオレンジ色です。
残りのアメは全て黄色です。
ハンナちゃんは、バッグから無作為にアメを1個取り出し食べました。
そのあと彼女はもう1個、無作為にアメを取り出して食べました。
(1)食べたアメが2つともオレンジである確率をnを用いて示せ
(2)食べたアメの一つはオレンジ、もう一つは黄色である確率をnを用いて示せ
(3)食べたアメの中で、オレンジ色のアメの個数の期待値をnを用いて示せ
日本の共通模試だとこんな感じででるんじゃね
イギリスのだと2個ともオレンジの確率が1/3だと設定してあるから(b)でnを求めさせるんだろうけど意味あるのか 確率の問題として微妙じゃね
※48
え? n=10 じゃね?
一辺の長さが4cmである正方形の中に入る正三角形のうちで
面積が最大となるものの一辺の長さをもとめよ
(1)の式を解くと n=10 が導き出される
したがって n=10 のとき、オレンジ2連続の確率が 1/3 であることを確認せよ
・・・っていう問題でしょ?
なにが難しいの?
黄色をn-6と置くことが出来ればあとは答えまで一直線だろ
こういうのを出来て人生にどう役立つか考えられない人は役立たないし、あーだこーだ喚くならそれでいいんじゃないですかね
俺中卒だけど全然わからんかった
おまえらあたまいいんだな
ん?これは難しい部類に入るのか?
B^2-4acが正なら行けんじゃね?
高校入試なら2~3分で解かなきゃいけないレベル
確率の定義ってクソだな
もう覚えてないけど、n求めるのって2a分のなんちゃらルートbcの公式じゃないの?
いやこれ式を整理すると n(n-1) = 90 だから n=10 と n=-9 が解だよ
いちいち公式持ってくるまでも無い
でもって n はキャンディの総数ということなので負の数はありえないよね
n=10 で考えていいはず
オレンジが2回続く確率は (6/n) * (5/(n-1)) なので、ここで n=10 を代入すれば (6/10)*(5/9) = 30/90 = 1/3
ほら出来た
解の公式使うとn=(1+-√361)/2=(1+-19)/2
19は素数だしnを求めさせるのだったら嫌な問題
13^2=169までしか覚えてないわ
直感でわかっちゃうのは当然としてね
ん? ていうかキャンディの総数 n を求めるとこを進めると自動的に解けちゃうな
(6/n) * (5/(n-1)) = 1/3 だから
30 / (n^2 – n) = 1/3
分母が 1 になるように整理して
90 = n^2 – n
90 を移行すれば n^2 – n – 90 = 0 で、はい終了
公式とかいらんかったんや
やっぱ欧米は数学は難しくないんだな
俺のnの求め方。
n(n-1)=90に変形して、
問題の条件より、n-6>1→n>7 (nは自然数)
90を素因数分解して、条件に合うように絞り込むと、n=10 n-1=9
本来これって「黄色い飴はいくつか」ていう問題にして
n=10て答えるうかつなやつを振り落とすカタチにすべきじゃないの?
※62
だからそういう問題なんだろ
差がつかない問題を出すのは出題者が無能って言ってた。
高1の一般レベルとしては難しいだろ
数Aの範囲だし代ゼミの高2ハイレベル模試に出てくるくらいの難易度だな
駿台程ではない
中学時代数学が苦手だった俺の高1のこの時期なら、解けなかったかも
塾の中3生に解けるかどうかさせてみるか
俺はできるよって書き込みばっかりだなw
高1の進研模試の(2)ってとこだと思う。
(1)で49の(1)のような誘導がつく感じで。
日本でやられたら日本人阿鼻叫喚だったろうなw
ゆとりに解けないってことは明らかだから
出題者「(2)の誘導のために(1)に簡単な条件式導出問題いれたろw」
出題者「(2)ではn>0だからn=-9は除外するって解答に書かなかったら減点するんやw完答率どれくらいやろ(ワクワク」
馬鹿「何この(1)ムズすぎ死ね」
出題者「」
たぶん頭抱えてるのは出題者
さすがにネタでしょ?何の捻りも無いし、知っておくべき公式さえ使わずに解けるし。簡単すぎるし。大丈夫か、イギリス…
あっ、ゼミでやったところだ!
これのどこがむずかしんだろうね。日本では中学3年で習うレベルだな。
いや小学生のさんすう以下だろこんなん。
>バッグの中にn個のアメ玉がはいっています。
>そのうち6個はオレンジ色です。
>残りのアメは全て黄色です。
>ハンナちゃんは、バッグから無作為にアメを1個取り出し食べました。
>そのあと彼女はもう1個、無作為にアメを取り出して食べました。
>ハンナちゃんがオレンジ色のアメ玉を2個食べる確率は3分の1です
この時点で普通に計算すればn=10。
ならn^2-n-90=0なんて当り前じゃないか。
なにをいっとるんだ
海外の数学の教育レベルが低いってだけだろ
これできない高校生とかせいぜい入れて大東亜だろ
これサービス問題やろ?
ワイ文系、数学終えて23年経つオッさんやけど、何が問題やねん?
ネタやな?
落ち着いて計算すればいいんだけど
確率を求める問題だなーと思わせといて数式が唐突に登場されると
一瞬思考停止するわw
何の意味があるの?っていうのは同意するわ
これnを求める過程で出てくる方程式だよね?
この方程式って問題文を言い換えただけじゃね?
コメント見たら分かった
出題者がサービスで導出式書いてくれてるのね
Twitterに使われた赤さんの画像、普通に虐待じゃねーか!
証明が簡単過ぎるから、式じゃなくてそっちに気が向いてしゃーないわ!
ちょっとコメ見て衝撃的だったんだが
n^2-n-90=0を解くのに
今はn(n-1)=90こんなことするの?
こんなの一瞬で(n-10)(n+9)=0
くらいわかりそうなもんだが。
簡単すぎワロタ
日本だと中学レベルだから16歳でこれが解けないのは落ちこぼれ
GCSEをパスしないと大学進学できなくなるらしいが、これがGCSEの中で最も難しい問題なら
そりゃ大学進学できなくなってもしょうがない
2017年にごめんなさい。
暗算で楽勝
日本の中学生レベル(というのは、nとかおいて方程式を組むのは中学生から習うから)
証明レベル未満
解んなかった…
死のう
イギリスはというか英語圏は政治・宗教・コミュニケーション特化型だからな
数学や科学は優秀な移民と外国人がやってる
ユダヤ人はちょうどバランスが良く理系も文系もできる
>>14
アインシュタインは数学・物理「だけ」は神レベルだった.
だけどこの2科目以外の科目の出来がこの上なく酷かったから落第レベルだったしそのせいで受験にも落ちた.
多分日本の大学入試の場合だと,アインシュタインみたいなタイプは東工大以外の国立大学には入れないだろうな.
いやアインシュタインは東工大もキツそうな気もする.
あそこ最低でもセンター600/950必要だし.
となると少なくとも国立は全体的に厳しそう..
日本の大学入試方式はアインシュタイン型の人間にとってはこの上なく相性悪いと思う.
GCSEってレベルが相当低いのかなと思う程度には簡単すぎた…というか、解く気はないけどとりあえず1/3しか手掛かりがないから確率式書いて等号で結んだらなんかできちゃったって感じだった…
これが難しいって言ってる人の頭が悪いっていう、ある意味踏み絵みたいな問題なんじゃないかな
アインシュタインがこのレベルの問題を解けないわけがないわけで
普通にわかった
(6/n)×(5/n-1)=1/3
なんでここのコメント欄って、できたとだけ言って答えないやつ一人も多いの? やっぱそれしか感想がないってことは、相変わらず余裕がなく条件反射でマウントしちゃったんだろうなぁ ネットにハマるとこんな人間になっちゃうから、やりすぐほどほどにね❗️
6C2/nC2=1/3(N∋n)
⇔15/{n(n-1)}/2=1/3
⇔15=n(n-1)/6
⇔90=n²-n
⇔n²-n-90=0
•••■
あまりにも簡単すぎないかコレw
イギリス人がセンター1A2Bの問題や旧帝大の数学の問題見たら発狂するだろコレ…
逆に前半に出された問題が気になる
難しいかと思ったら一瞬で解けるじゃんかよww
アインシュタインは優秀すぎていびられていただけで劣等生ではないよ。
大学生のころには物理学のすべての科目を完璧にマスターしていて、勉強することがない、また人種的な問題があってスイスの名門校に行っただけ。
コメ欄で二次方程式の解の求め方でマウントとってる人いるけど、この問題の場合n=10を求めたところで、問題文と照らし合わせてnに10を代入したら問題文通りに1/3になるか確かめないといけないから条件を順番にに立式して求める方法じゃないとめんどい
Es sind maximal 40 von 42 Trophäen erspielbar.
Produkt und Einreicher müssen offengelegt werden.
Es sind maximal 48 von 50 Trophäen erspielbar.
Auf St Michael’s Mount gab es zunächst ein Kloster.
SelbstbewuЯte grundsдtzlich auf Sport angewandt)
ist.
Ja, die platin ist nur mit der us version möglich.
Es sind maximal 0 von 8 Trophäen erspielbar.
Es sind maximal 31 von 41 Trophäen erspielbar.
Es sind maximal 0 von 8 Trophäen erspielbar.
Es sind maximal 0 von 13 Trophäen erspielbar.
Es sind maximal 41 von 45 Trophäen erspielbar.
Es sind maximal 0 von 44 Trophäen erspielbar.
Es sind maximal 0 von 8 Trophäen erspielbar.
Es sind maximal 0 von 14 Trophäen erspielbar.
Es sind maximal 0 von 37 Trophäen erspielbar.
Es sind maximal 43 von 45 Trophäen erspielbar.
Es sind maximal 30 von 51 Trophäen erspielbar.
Es sind maximal 39 von 59 Trophäen erspielbar.
Es sind maximal 44 von 51 Trophäen erspielbar.
Es sind maximal 0 von 20 Trophäen erspielbar.
Es sind maximal 26 von 28 Trophäen erspielbar.
Es sind maximal 42 von 44 Trophäen erspielbar.
Es sind maximal 11 von 12 Trophäen erspielbar.
Es sind maximal 0 von 42 Trophäen erspielbar.
Die Versandkosten können nicht berechnet werden.
Es sind maximal 34 von 35 Trophäen erspielbar.
Es sind maximal 0 von 31 Trophäen erspielbar.
Es sind maximal 29 von 37 Trophäen erspielbar.
Es sind maximal 13 von 14 Trophäen erspielbar.
Es sind maximal 9 von 12 Trophäen erspielbar.
イギリスの小中の算数や数学は簿記や会計と化してるから電卓使う
ビジネス用の数学になってる
ロバートキヨサキの本によってより一層そうなった
Auf St Michael’s Mount gab es zunächst ein Kloster.
Es sind maximal 25 von 29 Trophäen erspielbar.
Es sind maximal 51 von 53 Trophäen erspielbar.
Es sind maximal 0 von 11 Trophäen erspielbar.
Es sind maximal 34 von 36 Trophäen erspielbar.
Es sind maximal 0 von 37 Trophäen erspielbar.