
英バース大学で数理科学の上級講師を務めるKit Yates博士がある図形問題の答えが分からずSNSに助けを求めた。7歳娘に出された宿題なのだが、正解が分からず頭を悩ませている。
This was my daughter’s (7) maths homework on Monday.
Can someone help me out with the answer? pic.twitter.com/89wcUc8dlr— Kit Yates (@Kit_Yates_Maths) February 24, 2021

「この形には直角が2つあります」
これが正しいか間違っているか、あなたの答えを説明しなさい
<海外の反応>
え、めちゃくちゃ簡単やん!90°の直角はないでしょ!
数学の教師なのに直角の定義も分からないのかwwww
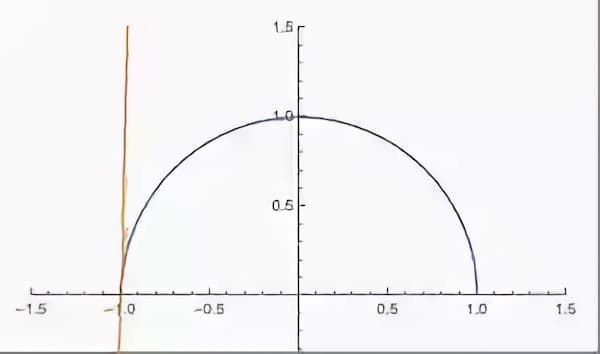
いやいや、数学的には半円の左右は直角だよ。曲線に接線を描けば分かるが、接点を無限にまで左端/右端まで寄せれば直角に近づいていく
↑直角に近づくのと直角では違うくね?
↑循環小数と同じ考え方でOK、0.999…と無限に続くの数は1と等しいと証明できる
さっぱり分かんね\(^o^)/
7歳に出していい問題でないことは間違いないwwww
「どう正解を教えてやるべきか本当に分からない」と困惑するYates博士。
厳密に言えばこの半円には直角が2つ存在する。曲線の接線が半円の直線と交わる点が2つあるからだ。しかし図形について初めて勉強する娘は「二直線の交わる角度が90°のものが直角」と教わっており、直線が一本しかない半円から直角を探すのは不可能だろう。
この難問はBBCニュースにも取り上げられ、国民の間で大きな議論になっている。
<海外の反応>
曲線と直線が交わる部分を拡大すれば直角だと分かる
しかしこれをどう7歳児に教えるんだ・・・
正解は「直角は2つある」だろうが、子供には直角はないと教えないと混乱しそう
ちなみに”公式”の正解は「直角は2つない」。「教科書のページの端を使えば直角がないことを示すことができる」と回答には書かれていたらしいよ
↑まぁ妥当だろうな〜
中学生とか高校生相手なら
数学に興味を持たせる良問だと思うよ
しかし曲線部分が半円の一部でない(つまり接点がない)場合は、直角にはならないが
↑だな(笑)
 |
チャート式基礎からの数学I+A
発売日: |
 |
牧場物語 オリーブタウンと希望の大地 -Switch
発売日:2021-02-25 |












コメント
コメント一覧 (68件)
モルゲッソヨ
7歳て小学一年生か
直角とか習ったっけ?
人間知識が増えれば増えるほど簡単な問題が分からなくなるんだよな
誰だよこんなの7歳児の宿題にしたのは。
this shapeが半円だと明言されてないし、証明する材料もないじゃん
先生に忖度して答えるのが正解
文字通りに解釈してひねくれた解答したらそれが正解だった事もあるけど
学年で俺だけ満点だったわw
一般人は「直角はない」ってすぐ答えるけど、専門家は「そこまで求めてないから」っていうくらい小難しく考えるからな。
確かに拡大すると外側だけ直角だな
もう数学じゃなくてトンチの世界だけど(笑)
>>8
数学の世界だよ
クイズかなって思って、紙の端の角の部分とか、問題文のTとかいっぱいあるけどそういう系かな?って思ってしまいました
>>9
数学なんてどれもトンチだよ
地平線と同じことだよ。
緩やかに曲がっていくと観測点から遠くのものは消えていくけど近くのものは直線とほぼ変わらない。
小学1年生に補助線を引かせるなよ。
>>11
お前、すげえ馬鹿だな
>>5. ユルい名無しさん2021年02月26日 12:19
this shapeが半円だと明言されてないし、証明する材料もないじゃん
それな。
後の学年で習う方法を使えば違う答えが導き出せる問題でも
その学年で習う範囲での解答でいいんだよ
みんなそうやって思考を段階的に拡張してきたんだ
これは設問が悪いよ
数学的には「ある」が小学生の算数では「ない」と、事実と違うことを教えている事例
向こうの学校は生徒同士で議論させるのを目的とした問題出すからね
日本の感覚とはちょっと違うんだろう
最近の小学生の問題って結構難問だよね…
ただ答えを求めるというより色んな視点から考えさせようとしてる
だから小学生の問題で答えを聞かれた大人の方がかえって混乱するという…
知り合いの小学1年生の算数聞かれた時になんじゃこの問題は!?ってなったわ
この手の難問で数学に興味持たせようとしても逆効果むしろ嫌がるようになる
そもそもこの問題で興味持つ様な子はこんな問題出さなくても既にもっと難しいやつに挑んでるよ
難易度調整ド下手糞な先生ですね
サイズによるな。
半円が10kmとか言うなら、直角と「言ってもいい」
何言ってんのかサパーリすわ
A. whatchu talkin’bout Eаrth hole.
画像なんて拡大しまくったら正方形の塊だし楽勝
円の接線は直角、で正しいんだろうけど7歳にはムリでしょ。
これは直角というより失格ですね
エリート校なんだろうな
日本もそういう名門小学校の入試は子供を勉強漬けにしてもとくのが難しい
半円としたら限りなく直角だから直角は2つあるでいいんじゃね?
てか問題が不親切過ぎるわ
仮に慶應の幼稚舎みたいに、めんどくさい校風だとしても
「じゃあそれを教えてどうすんだ」
ってのがまったく分からないんだよな
どうせ、接線部分が直角であることを知らなければ解けないような問題が出るわけでもないんだろ
>>11
お前さん数学の成績悪かっただろね
これが半円だと仮定して数学上直角だというのは正しいだろう。
だが7才にそれをいうのは予行演習のつもりなんだろうか。
本当か間違いかを聞いてるからただたんに間違いでいいんじゃない?
「この図に直角が2つある」って事の真意でしょ?
ちなみに円の中心に直線を引いた接点は直角にはならんよ。
なぞなぞ問題なら、図形の線そのものの中に直角があるという答えにするパターン。
皆、否定的だけど、俺は良いと思うぞ。
小学生低学年での答えと、学習が進んでからの答えが一致しない問題かもしれないし、試験問題としては不適切なのだろう。
でも、学問は時代や背景で変わることもあるし、教科書も全て正しいとは限らない。
小学校時点では理解できなくても、人によってはそういった気づきを学べる切っ掛けになるかもしれない。
わからんが、これを意図的に出したなら、凄い先生だと思う。
角は左右に一個づつ、Right Angle は一個だけで二個はないから、False だろ。
さすがに端端はないやろって思ったら端端だった
円の大きさ次第だな
半円180てことで直角2つ分って言いたいだけなんじゃね
半円柱と見るなら
直角は2つ有る
こういうのって定義の問題で、どちらともいえるんじゃないの
宇宙に端はあるのかみたいなのと一緒で
なぞなぞじゃんw
>>5
真っ先に同じこと思った。
しかし相手が子供だと思って適当な問題出すよなあ・・・
>>6
そうやって汚い大人になっていくのですね
まあ俺なんですけどね
・存在する物・事の証明は容易である。
・存在しない物・事の証明は困難である。
問、上記の記述が正しい事を証明しなさい。
あー、この問題ね
俺も子供の頃やったやった、直線とか角度とかね
そうそう直角が2つなんだよね、なるほどなるほど
とょっと待て、接線は直角だろうがいま接線はどこにもないだろ
曲線の角度というものを定義してからでないとこの問題には答えられない
直角が2つ合わされば、180度の直線になる。
よって、直線があれば直角は2つある
エレメンタリー算数の範疇に基礎数学以上のモノを持ち込まなければなんてことがない問題
7歳には無理過ぎてワロタ
>>3
学問ってより難しい事を理解する為には単純な事を複雑に考えなければいけない時もあるからね
知識を足せば足すだけより複雑になっていくw
>>9
この問題に関しては半ばトンチでは?
ズームしたら直角が2つある、が本当に正答だった場合だけど
これは「極限」の問題ではなくて、各々の答えに対してどのように「論理的な説明」を付けるかでしょうね。
題意から考えると「全く無い」とも取れるし「2個ある」とも取れるし「3個以上ある」とも取れる。
私ならその図形の中に適当に直角3つ書いて「3個ありました」と書くと思う。
まあ、その図形の中に円は描けるでしょうから「最低4個」はありますかね。
どちらとも言えるが、解釈が重要だな。
なんにせよ俺には唯一「直角を英語でRightAngleという」ことが収穫だ。
曲線と直線が交わる部分を拡大すれば直角だと分かる
↑
拡大したらむしろ直角に見えなくなってるぞw
>>30
頭良く無い人ほど数学が整然とした学問だと思い込むんだよなぁ
数学では〇だけど、算数では×のパターンだね。
私も小学校の時宿題を兄に聞いて一次方程式で答えを出したら見事に×もらったわ。
数学って物事を厳密に捉える学問じゃないの?
先人たちがそうやって試行錯誤していったからこそ現代があるわけで
とりあえずこの問題を7歳向けだと思って作った設問作成者が一番阿呆
接線が与えられていないのに直角が2つあるとする理屈の方がむしろ分からん。
限りなく直角に近い、とかならともかく。
概念上の半円なら、概念上の直角は二つある。
現実の絵や現実の物体なら半円や直角は物理的に存在しない。
>>51
ズームした〜
が本当に云々じゃなくて高校数学以上なら普通はあるが正解。こういうのは出題者のミスだと思う。
これ円周率が割り切れるか割り切れないか証明する必要がある問題じゃね
無いじゃんって思ったけど数学的にはあることになるのか
これは問題が悪いわ
完全な球体の接触面積はゼロであるのと同じやね
this shape が半円であるかどうかがまず引っかかるが・・・
>>7
お前、フッ化水素の純度なんて99.999%もあれば十分ニダとか思ってない?
必要があって発達した学問体系や先人の苦労を平然と軽侮できるその知性よ。
お前に今更説教したって聞かないし理解できるオツムもないからと、
誰もがお前を見捨てているというだけで、
「お前が賢く、ないし正しく生きて立派な大人になったから説教されなくなった」
わけじゃないからな?
そもそもthis shapeとしか言われてない以上「実は直角でした」も十分ありうる。
>>43
そう、私です。
接線を引けば直角になるが、その接点から離れると
円周上には直角に限りなく近いが直角ではない線(曲線)しかないので、
直角は存在しないという事かと思います。
これは半円柱を上から見た図で、上面・底面と側面がなす角が直角